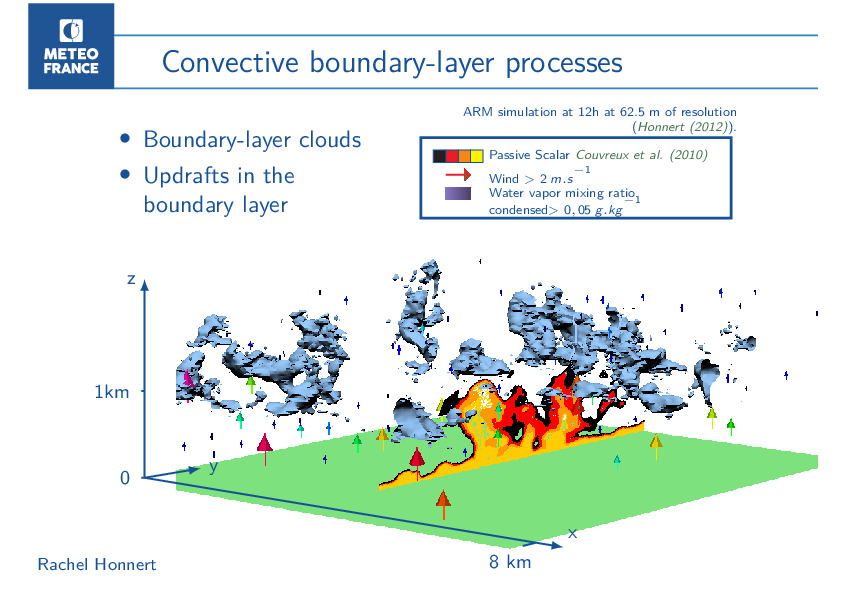
Atmospheric turbulence ranges over very various scales, from typical turbulence production scales (those of the largest eddies as boundary-layer thermals that stretch from the bottom to the top of the boundary layer) to eddy sizes where molecular forces disperse the turbulent kinetic energy.
Vertical cross-section in LES IHOP.
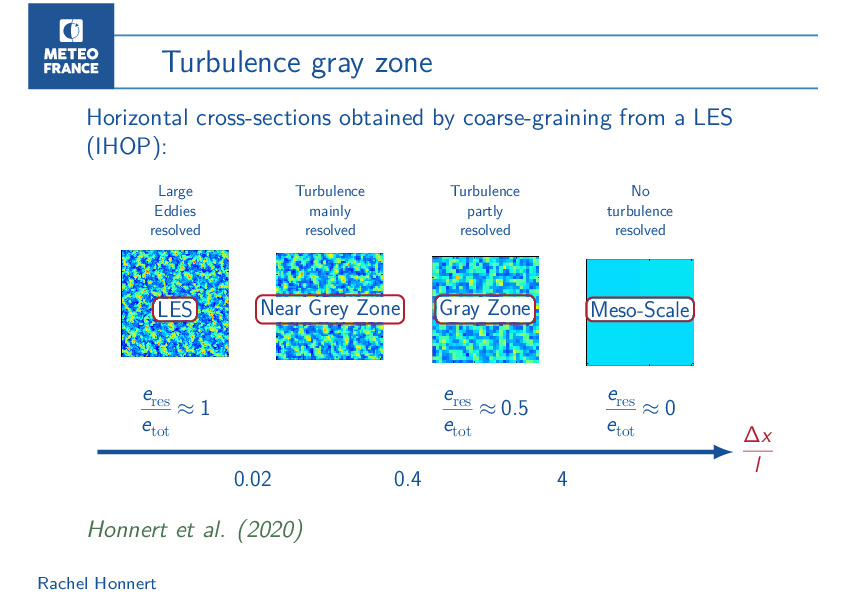
Turbulence modelling in atmospheric transfers is essential as eddies both impact mean flows by mixing, as well as disperse turbulent kinetic energy into internal energy by friction at the ground. Turbulence is well-represented by atmospheric models for very fine meshes, from 10 to 100 m, for which turbulent movements are mainly resolved, and for large meshes, coarser than 2 km, for which they are entirely parametrized. But what happens at intermediate sub-kilometric scales ? My research themes have focused on questions of representation of atmospheric turbulence at hectometric scales.
Gray zone of turbulence
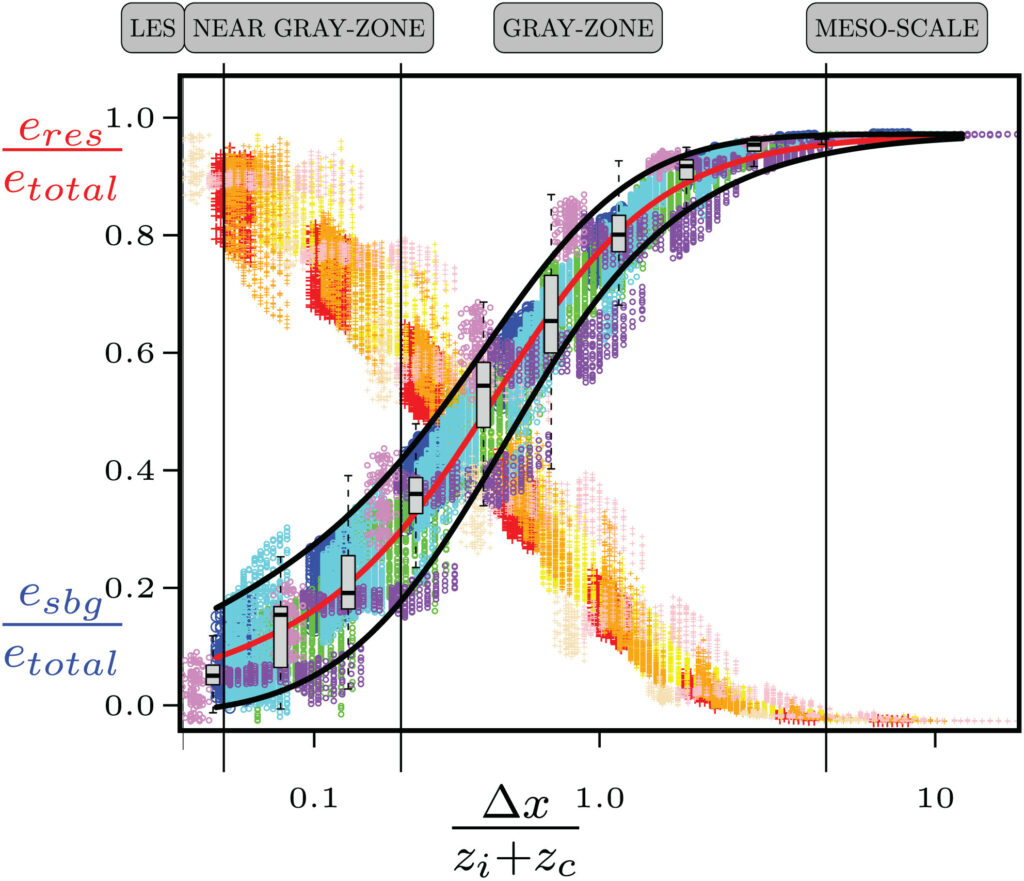
In 2009, I had the opportunity to do a PhD thesis under the direction of Valéry Masson on this topic. The aim was to document the characteristics of the boundary-layer turbulence in the resolution range where the turbulence is not yet fully resolved, but more fully sub-mesh: the gray zone of turbulence. It was necessary to prove its existence, to define the range of impacted resolution and its characteristics on various parameters, to quantify the defects of the physical mesoscale parameterizations (1-10 km of resolution) and to find some solutions. I quantified the correct resolved and subgrid parts of eddies in dry and cumulus-topped convective boundary layer at sub-kilometric scales using Large-Eddy Simulation (LES). Thanks to this diagnostic I determined the error in the modelling of resolved/subgrid partition of the Méso-NH model, a state-of the-art model. Simulations satisfactorily reproduce the partition until 125-m resolution. Likewise, for coarse grid size (up to 4000 m), the totally subgrid partition is well-represented by Méso-NH (the whole turbulence is subgrid). However, intermediate scale were poorly represented.
Link to my PhD-thesis (in French).
In 2012, I joined the ‘Process’ team of CNRM/GMAP at Météo France on questions of alleviating the defects of the models at the hectometric scales. In mesoscale numerical weather prediction models, such as Météo-France’s AROME, the resolution does not explicitly resolve atmospheric turbulence. It is then a question of correctly taking into account the impact of these vortices on meteorological phenomena of a larger scale. The so-called subgrid physical phenomena, such as turbulence, are modeled via physical parameterizations. Nowadays more efficient computers make it possible to reach hectometric resolutions. But at these scales, the models are in the gray zone of turbulence. The heart of my research work consists in evaluating and adapting models to these scales. I therefore seek to improve the representation of physical processes, and in particular the modeling of shallow convection, as part of a steady increase in the resolution of all forecasting systems.
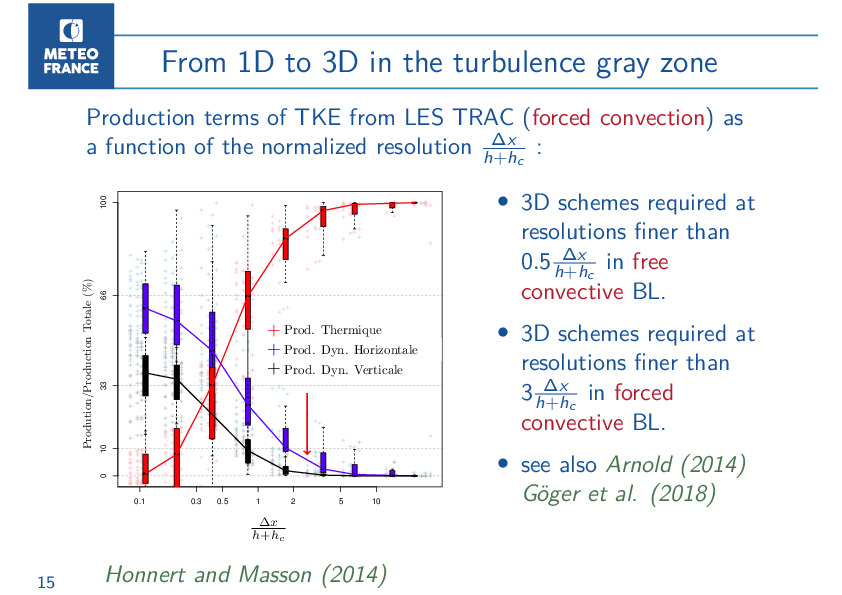
Need for Turbulence 3D
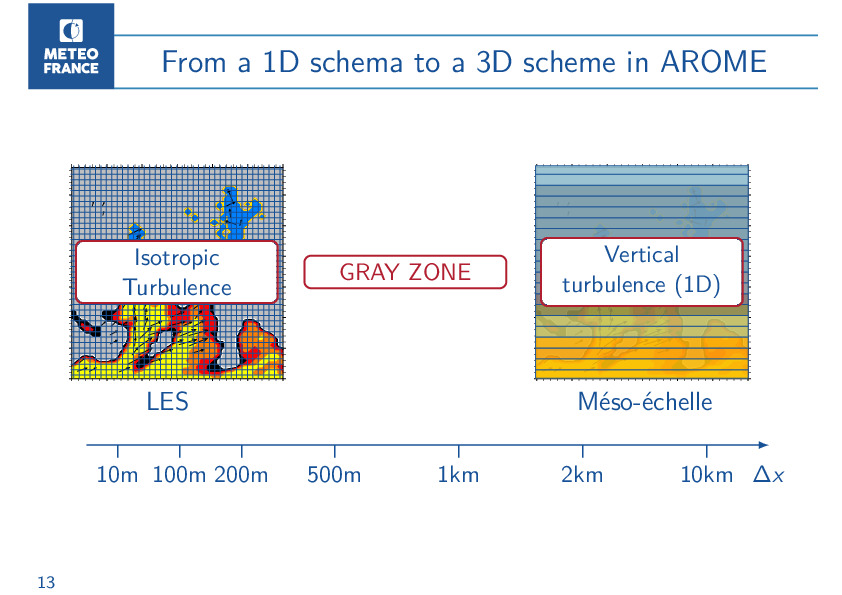
At the same time, other questions about the gray zone of turbulence have emerged. By increasing the resolution of models again and again, more and more processes are solved. The parametrizations must simulate the residual turbulence which then takes on characteristics different from that of the mesoscale. In particular, under the hypothesis of horizontal homogeneity, the parametrization of the turbulence will homogenize the fields on the vertical only. This is valid on a large scale where the fields are much more heterogeneous on the vertical than on the horizontal. At hectometric scales, the horizontal inhomogeneities become important and we have to start modeling the turbulence in 3D. However, this horizontal homogeneity assumption is important for weather forecasting models, because it allows good optimization of the code and its abandonment poses significant technical difficulties. And once again, the story won’t end there. Once the boundary layer thermals are resolved, the residual turbulence is essentially three-dimensional, yet it is not isotropic, as is assumed at very high resolution. They concern smaller scales (<500m) which are far from those of the current numerical forecast. But for how long ?
Finally the size of the turbulent subgrid eddies is described in the parametrizations of our numerical weather prediction systems by a length, known as the mixing length. There are dozens of ways of representing this length. In LES, it is of the order of the mesh size, sometimes limited by stability. In mesoscale models, it is of the order of the size of the largest turbulent eddies. But what is this length worth in the grey zone? In LES, turbulence is assumed to be isotropic, but in the mesoscale it is assumed to be purely vertical.
Nevertheless when we start to look at the anisotropy of turbulence, we can get into the throes of complexity. Simplicity is a strength in parameterisation. We therefore propose a length as a mixture between BL89 used in AROME and DEAR used in LES (Honnert et al., 2021).
In 2022, I passed my HDR (Habilitation à Diriger des Recherches) to supervise research in the field of the atmospheric Sciences. Link to my HDR (in French).
In 2023, I was leading a group working on a configuration of AROME-500~m over Paris and Marseille and as part of an ACCORD group on very high resolution and in the framework of 2024 Paris Olympic games.
